超几何分布是统计学上一种离散概率分布。它描述了从有限N个物件（其中包含M个指定种类的物件）中抽出n个物件，成功抽出该指定种类的物件的次数（不放回）。称为超几何分布，是因为其形式与“超几何函数”的级数展式的系数有关。 [1]

超几何分布中的参数是M,N,n，上述超几何分布记作X~H(N,M,n)。

定义

编辑

产品抽样检查中经常遇到一类实际问题，假定在N件产品中有M件不合格品，即不合格率

。

在产品中随机抽n件做检查，发现k件不合格品的概率为

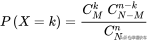
,k=0,1,2...min{n,M}。

亦可写作

（与上式不同的是M可为任意实数，而C表示的组合数M为非负整数）

为古典概型的组合形式，a为下限，b为上限，此时我们称随机变量X服从超几何分布（hypergeometric distribution）。

需要注意的是： [1]

（1）超几何分布的模型是不放回抽样。

（2）超几何分布中的参数是M,N,n，上述超几何分布记作X~H(n,M,N

示例

已经知道某个事件的发生概率，判断从中取出一个小样本，该事件以某一个机率出现的概率问题。

例：在一个口袋中装有30个球，其中有10个红球，其余为白球，这些球除颜色外完全相同。游戏者一次从中摸出5个球。摸到至少4个红球就中一等奖，那么获一等奖的概率是多少？

解：由题意可见此问题归结为超几何分布模型。

其中N = 30. D = 10. n = 5.

P（一等奖） = P(X=4) + P(X=5)

由公式

,k=0,1,2,...得：

P（一等奖） = 106/3393

期望

定理：对超几何分布X~H(N,M,n) ，随机变量X的数学期望

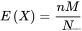
. [2]

引理一：

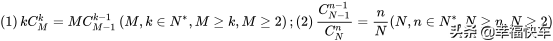
引理二：

引理证明：它们均可用恒等式（1+x）M-1(1+x)N-M=(1+x)N-1两边的展开式中含xn-1项的系数相等证明。仅以（2）中n≤M的情形证明如下：

的展开式中含xn-1项的系数为（注意N-M

定理证明：当M=N=1时，X的分布列P（X=1）=1，且有n=1，可得此时欲证成立。

当M=1，N≥2时，X的分布列为：

所以

（引理一(2)）

下证M≥2时也成立，又分两种情形：

（1）又当n≤N-M时，X的分布列见超几何分布的定义有

（2）又当n>N-M时，X的分布列见超几何分布的定义有

因此定理获证 [3]

方差

对X~H(N,M,n)，

[4] .

证明：D(X)=E(X2)-E(X)2 （此公式利用定义式简单展开即得）

（提取，变形）

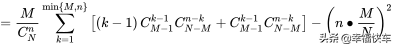
（拆项，变形）

（拆开∑，就是分组求和）

[2] （化简即得）

超几何分布和二项分布的联系 [1]

（1）在超几何分布中，当

时，

(二项分布中的p）。

（2）当

时，超几何分布的数学期望

（3）当

时，超几何分布的方差

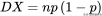
（二项分布的方差）。

（4）当

时，超几何分布近似为二项分布。