100次浏览 发布时间:2024-08-27 10:34:54
假设一笔投资的回报情况是第一周盈利1元,第二周盈利10元,第三周盈利100元,那么每周盈利的均值=(1+10+100)/3=37元。
在这里,均值体现的是收益率分布的中心在哪里,但并没有体现出收益率的分布差异程度。因此在衡量一组数据的分布情况时,不能只看数据的集中程度,为了量化该组数据中某一具体数值分布的精确度以及与其他数据的分布偏离程度,需要借助一些衡量数据分布差异性的指标。
数据区间
数据区间是指该组数据中最大值和最小值之间的距离。
比如有三组数据:
1、(1,1,1)
2、(1, 1,2)
3、(1,2,3,4,5,100)
第一组数据分布的差异程度为1-1=0;第二组数据分布的差异程度为2-1=1;第三组数据分布的差异程度为100-1=99。在第三组数据中,分布差异最大的是100-1的99,但99并不代表第三组中各数据之间一般的分布情况,因此数据区间只体现数据组中最大值和最小值之间的差异程度而没有考虑数据分布的集中趋势。
均值偏差
均值偏差是指一组数据中各数据与均值之间的差异程度。
以下是另两组数据:
1、(5,5,5)
2、(6, 7,1,6,5)
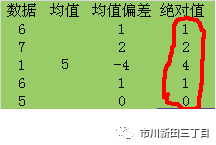
这两组数据的均值均为(5+5+5)/3=(6+7+1+6+5)/5=5,如果计算一下各数据与均值5之间的差异程度就可以看出均值5是否很好地代表了整组数据的分布情况,如下图所示。


在第二组数据中,差异程度最大的是数据1与均值5之间的4,最常见的差异程度是1,因该差值出现的频率最高。
如何用一个数据来表示一组数据均值偏差的程度?如果将各数据的均值偏差值相加,结果肯定是零,因此解决方案有两个,以第二组数据为例:
第一、是将差值的绝对值相加,那么绝对值之和为8。

第二、是求该组数据中每一个数据的均值偏差的平方的和,那么均值偏差的平方的和为22。

在这两种解决方案中,第二种方法被认为更好一些,但22这个数字只是该组数据中各数据的均值偏差的平方的加总,既没有体现出数据分布的差异程度也没有体现出均值在代表数据分布情况方面的准确程度。
方差
方差是用一组数据中各数据的均值偏差的平方的和除以数据的总数
第二组数据的方差等于22/5=4.4,说明第二组数据中各数据的均值偏差的均值为4.4,但方差这个指标也有局限之处,第二组中均值偏差的绝对值最高的才是4,而4.4比4还高,因此方差用来描述数据的分布差异未免不太精确。
标准差
方差指标的缺陷导致标准差这个指标的登场,标准差是方差的开方,标准差具有方差的一切优点,但又规避了方差指标数值过大的弊端。

标准差=4.4^0.5=2.0976
中位数绝对偏差
与均值偏差这个概念非常相似的是中位数偏差,对一组数据中的各个数据按大小排序后处于中间位置上的数值即为中位数,计算各数据与中位数的差值,再对差值的绝对值进行大小排序,其中位数即被称为中位数绝对偏差,本例中为1,可以用Excel的MEDIAN函数计算得出。
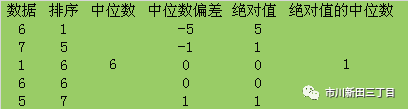
与标准差相比,中位数偏差的绝对值更适合数据组中存在异常值的情况,因为标准差还是来自于均值偏差的平方,因此偏差大的数据对标准差的影响权重更大。而如果偏差较大的数据总量不多,对于中位数偏差的绝对值排序不会产生大的影响。
以标准普尔500指数的周度收盘价数据为例看看这几个指标在衡量数据分布方面的差异。

数据区间:
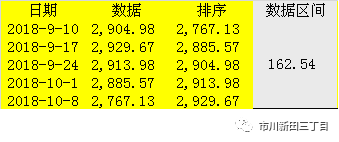
均值偏差:
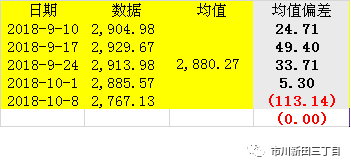
方差和标准差:
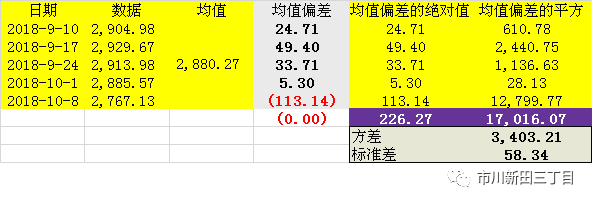
中位数绝对偏差:



