公式

曲率半径：

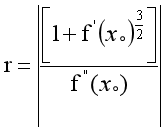
曲率半径公式

曲率中心：

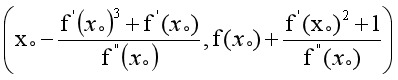
曲率中心公式

定义

类比于圆的两切线的垂直平分线交于圆心，我们假设任一曲线无限接近于一点P（x。，y。）的两切线的垂直平分线也交于一点，如下图

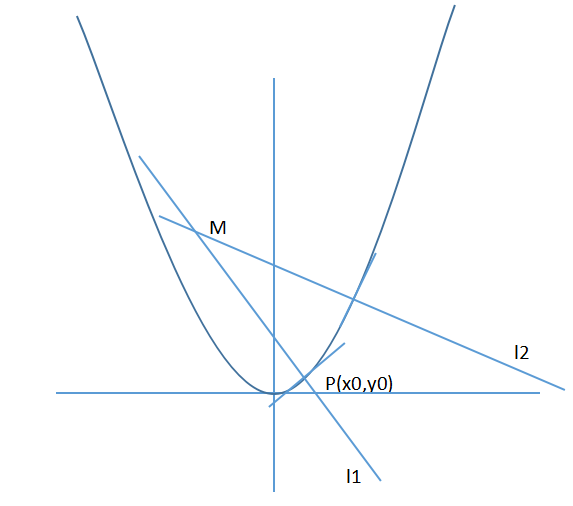
示例图形

推导过程

有了定义，那我们就直接开门见山，开始推导曲率中心的公式吧：

l1：y-f(x。)=-(1/f'(x。))(x-x。)

l2：y-f(x。+Δ x)=-(1/f'(x。+Δ x))[x-(x。+Δ x)] ,其中Δ x->0

我们把y消去后就可以得到

f(x。)-(x-x。)/f'(x。)=f(x。+Δ x)-[x-(x。+Δ x)]/f'(x。+Δ x)

移项得

{[f'(x。+Δ x)-f'(x。)](x-x。)-f'(x。)Δ x}/(f'(x。)f'(x。+Δ x))=f(x。+Δ x)-f(x。)——（1）式

由于当Δ x->0时，有

f'(x。)=[f(x。+Δ x)-f(x。)]/Δ x

f''(x。)=[f'(x。+Δ x)-f'(x。)]/Δ x

因此（1）式等号两边同除Δ x->0得

[f''(x。)(x-x。)-f'(x。)]/(f'(x。)f'(x。+Δ x))=f'(x。) ——（2）式

由于Δ x->0，

因此,f'(x。+Δ x)=f'(x。)

所以（2）式可以写成

[f''(x。)(x-x。)-f'(x。)]/(f'(x。)^2)=f'(x。)

移项得

x=x。-[f'(x。)^3+f'(x。)]/f''(x。)

代入y-f(x。)=-(1/f'(x。))(x-x。)得

y=f(x。)+[f'(x。)+1]/f''(x。)

至此，曲率中心的公式就推导出来了

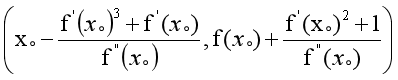
曲率中心公式

由距离公式得

r=|PM|，其中P的坐标是（x。，y。），M的坐标就是曲率中心，我们不难得到曲率半径的公式

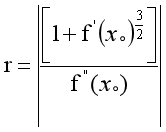
曲率半径公式